�x�ı��b�ù��r�c������Д�(sh��)�ⷨ�͈D�ⷨ�ɷN������
һ���D�ⷨ
�D�ⷨ����������ֱ�^���ڹ����Б�(y��ng)���^�V����
�D1���x�ı��b�õĹ��r���������ˮ�Øӱ����ṩ��Q-H���������ٰ���ʽH=Hst+∑h�������Hst�ĸ߶���������������ܵ��pʧ��������Q-∑h,�ɗl�����ཻ��M�c�������M�c��ʾ��ˮݔ�����߶Ȟ�Hst�r�����ˮ�ù��oˮ�Ŀ����ܣ��c�ܵ���Ҫ��Ŀ�������ȵ��ǂ��c�����Q����ԓˮ���b�õ�ƽ��r�c��Ҳ�Q�����c����ֻҪ���l�����l(f��)��׃��������ˮ���b�Ì���(w��n)�������@�c���������ˮ����Qm,�P�̞�Hm���
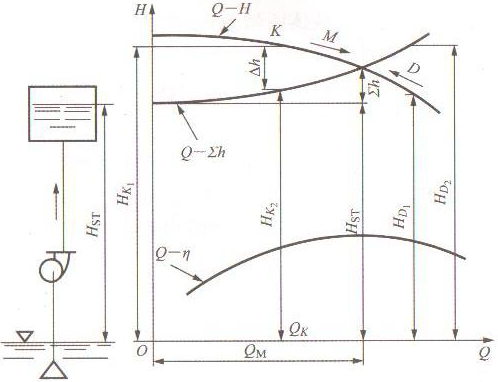
�D1 �x�ı��b�õĹ��r
���O(sh��)���r�c����M�c������K�c����ЈD1��Ҋ����(d��ng)������Qk�r������ˮ���܉oˮ�Ŀ�����Hk1��������Ҫ��Ŀ�����Hk2����Ҳ���۹��o�ݣ�����Ҫ��������������ԣ�ˡ�hֵ���˸�ԣ���������Ԅ��ܵ���ʽ������ʹ�ܵ���ˮ�����٣������Ӵ�������ɴ�������ʹˮ�õĹ��r�c���Ԅ������������һ��(c��)�Ƅӣ�ֱ������M�c��ֹ������֮���������O(sh��)ˮ���b�õĹ��r�c����M�c����D�c��������ô�Y(ji��)��ˮ�ù��o�Ŀ�����Hd1��С�ڹܵ���Ҫ��Ŀ�����Hd2,Ҳ���۹��o�ݣ�����Ҫ�ݣ��ܵ���ˮ����������������������p��������ˮ���b�õĹ��r�c���������pС��һ��(c��)�Ƅӣ�ֱ���˻�M�c���_(d��)��ƽ��������ԣ�M�c����ԓˮ���b�õĹ��r�c����������ˮ���b����M�c�����r���ܵ��ϵ������l�y��ȫ�_����������ô��M�c�ͷQ��ԓ�b�õĘO���r�c������Ҳ�����f�����@���b�����������Ҫ���Cˮ�õ��o�P�̞�Hst�r��������ܵ���ͨ�^�����������Qm�����ڹ����������҂�����ϣ��ˮ���b�õĹ��r�c�܉�(j��ng)������ԓˮ�õ��O(sh��)Ӌ����(sh��)ֵ������@���������ˮ�õĹ���Ч����ߣ��Ï�����Ҳ�(j��ng)��(j��)����
Ҳ�������������ķ�����Ҳ�Q“��������������”������ԓˮ���b�õĹ��r�c��������D2��ʾ������Q����(bi��o)�S�����残��ԓ�ܵ��pʧ��������Q-∑h����������ˮ�õ�Q-H���������Ϝpȥ����(y��ng)�����µ�ˮ�^�pʧ���õ���Q-H��´����������ˣ�Q-H��´�����Q����������������������������ϸ��c�Ŀv����(bi��o)ֵ��ʾˮ���ڿ۳��˹ܵ�������(y��ng)�����r��ˮ�^�pʧ�Ժ���ʣ�����������@�����H�Á���׃������ˮ��λ��������������ˮ������Hst�ĸ߶���ȥ���������ˣ���ˮ��ˮλ��һˮƽ�������c��Q-H��´�����ཻ��M1�c�������M1�c�v����(bi��o)������ԓ�b�õ��o�P��������M1�c����������������Q-H�����ཻ��M�c�����tM�c�Ŀv����(bi��o)ֵHm��������ԓˮ�õĹ����P��Hm=Hst+∑h���������ǹܵ���Ҫ�Ŀ������cˮ�ù��o�Ŀ�����������ȵ�һ�c���M�c�Q��ԓ�x�ı��b�õĹ��r�c�������������(y��ng)��������Qm���
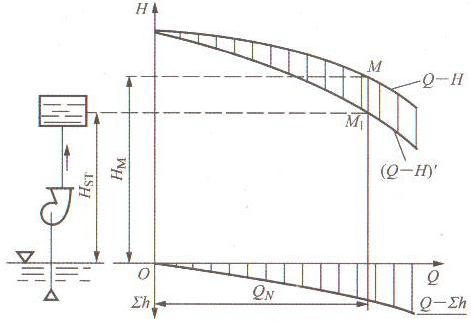
�D2 ���������������r�c
��ˮ�õ����������������Π��������t���c��·���������Ľ��c���ܳ��F(xi��n)�ɂ�����D3��ʾ�����������ˮ�����������½��εĽ��c�鷀(w��n)�������c�������������εĽ��c�t�Dz���(w��n)�������c������ˮ����K�c������������ij�Nԭ��ʹ�����c�x�_K�����Ƅ���������t����������������������ӣ�ֱ��Խ�^픷�������½���ijһ�c����M�c���ŷ�(w��n)��������֮�����c�����Ƅ�������t����������(y��ng)���������ʹ�����pС�������ֱ�������������ֹ�������������֪������һ�������ɔ_��������c�x�_K֮����Ҳ�����ص�K�c�����HK�c����������������������ζ����@�N��r������������ˮ�������������������Dz���(w��n)�������^(q��)�����\�Еr��(y��ng)���_�˅^(q��)������ֻ���½��β��Ƿ�(w��n)�������^(q��)��
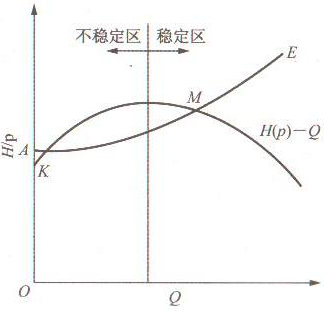
�D3 ˮ�ò���(w��n)�������^(q��)
�������(sh��)�ⷨ
�x�ı��b�ù��r�c�Ĕ�(sh��)�⣬�䔵(sh��)�W(xu��)����(j��)����Ώ�ˮ�ü��ܵ�ϵ�y(t��ng)�������������н��Q��Hֵ��������������Ѓɂ��������Q����Hֵ��H=f(Q) ��4�� H=Hst+∑KQ² ��5��
��ʽ��4�����ʽ��5����Ҋ���ɂ�������ɂ�δ֪��(sh��)����ȫ���ܵ��������P(gu��n)�I��������_��ˮ�õ�H=f(Q)����(sh��)�P(gu��n)ϵ��
�F(xi��n)���O(sh��)ˮ�ÏS�ӱ������ṩ��Q-H�����ϵĸ�Ч���������������з��̵���ʽ����ʾ��H=Hx-hx (6)
ʽ�У�H��ˮ�õČ��H�P�̣�m����
Hx��ˮ����Q=0�r���a(ch��n)����̓���P�̣�m�������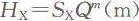 ����� �����
hx������(y��ng)��������Q�r���Ã�(n��i)��̓ˮ�^�pʧ֮�����
Sx����w��(n��i)̓���ϵ��(sh��)��
m��ָ��(sh��)��������oˮ�ܵ�һ��m=2��m=1.84����
�F(xi��n)����m=2����t��H=Hx-SxQ² ��7��
�D4��ʽ��7���ĈDʾ��ʽ����������ˮ�õĸ�Ч��ҕ��SxQ²������һ���M�ɲ���������������L�c�v�S�ཻ��Hxֵ������Ȼ���������ڸ�Ч��(n��i)�����x����c������(bi��o)������ʽ��7�������˃��cһ���ܝM��˷���ʽ�����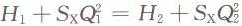
����һ�_ˮ�ö���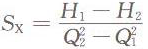 ��8�� ��8��
��H1��H2���Q1��Q2����ֵ֪�������ʿ������Sxֵ����ʽ��8������ʽ��7���ɵã�Hx=H1+SxQ² (9)
��ʽ��9���������Hxֵ������1�г���SA��̖�x�ıõ�Hx�������Sxֵ�������(j��)�@Щ��(sh��)��(j��)���Ϳ��Ԍ���ˮ�õ�Q-H������������ʽ��H=Hx-SxQ² ��10��
��1 SA��̖�x�ıõ�Hx��Sxֵ
|
ˮ����̖
|
�D(zhu��n)�٣�r/min��
|
�~ֱ݆����mm��
|
m=2
|
|
Hx/m
|
Sx(s/L) ²/m
|
|
6SA-8
|
2950
|
270
|
112.76
|
0.00715
|
|
6SA-12
|
2950
|
205
|
61.67
|
0.00407
|
|
8SA-10
|
2950
|
272
|
107.40
|
0.00233
|
|
8SA-14
|
2950
|
235
|
79.41
|
0.00288
|
|
10SA-6
|
1450
|
530
|
100.43
|
0.000286
|
|
14SA-10
|
1450
|
466
|
76.25
|
0.0001
|
|
16SA-9
|
1450
|
535
|
105.19
|
0.000075
|
|
20SA-22
|
960
|
466
|
29.54
|
0.000028
|
|
24SA-10
|
960
|
765
|
92.13
|
0.0000234
|
|
28SA-10
|
960
|
840
|
115.67
|
0.0000151
|
|
32SA-10
|
585
|
990
|
59.29
|
0.00000529
|
|
�潭56-23
|
375
|
1200
|
30.29
|
0.00000042
|
|
12H��c
|
1450
|
460
|
76.50
|
0.0001
|
|
14H��c
|
1450
|
529
|
102.90
|
0.000088
|
|
20H��c
|
960
|
765
|
92.90
|
0.000024
|
��(d��ng)�x�ıù����r��������ʽ��5����ʽ��10���ɵã�Hx-SxQ²=Hst+∑KQ²
Ҳ��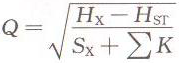
ʽ��Hx��Sx��∑K������ֵ֪�����(d��ng)Hstһ���r���������ˮ������(y��ng)���r�c�������͓P��������
��������ʽ��10���Ľ������ǰ�ˮ�õĸ�Ч��ҕ����Β��タ�ϵ�һ������������@�N��ʽ������Q-H��������������������Q�钁�����������������H�ϲ�����ÿ�_ˮ�õĸ�Ч�ξ��ܝM����O(sh��)�l���ġ��@�ӣ��ڌ��H�����о͕�����һ�����`�����
�M���x�ı�Q-H�������̵���һ;���Dz�����С���˷����M(j��n)�С��҂����ߵȔ�(sh��)�W(xu��)�е���С���˷������c�x�ı�Q������H���p׃���P(gu��n)ϵ�У��������̽M�Ɍ��ɣ�.png) ��12a�� ��12a��
�M���x�ıõ�Q-H�����������̿ɰ���ʽ��ã�H=H0+S1Q+S2Q² ��12b����H=H0+S1Q+S2Q²+S3Q³ ��12c��
����ʽ��12b��һ����������������ʽ��12c�������^�ߣ����������������
��1 �F(xi��n)��14SA-10���x�ı�һ�_���D(zhu��n)��n=1450r/min��������~ֱ݆��D=466mm���������Q-H����������D5��ʾ�����ԇ�M��Q-H�����������������
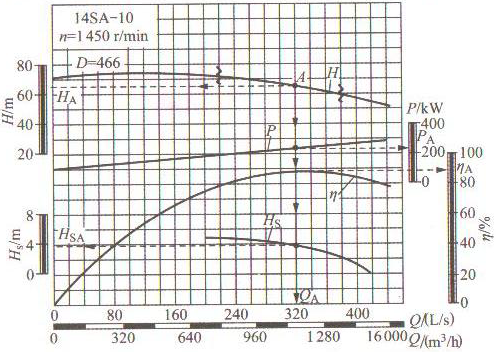
�D4 14SA���x�ıõ���������
�� ��14SA-10�͵�Q-H��������������ȡ������Qo����Ho���ڃ�(n��i)���������c����ֵ���2��ʾ�����ϱ���Hֵ��λ��m����Qֵ��λ��L/s����
��2 �Ă����r�c�ģ�Q�����H�� ֵ
|
��̖
|
��֪���c������(bi��o)ֵ
|
����(sh��)Ӌ��ֵ
|
|
Ho
|
Qo
|
H1
|
Q1
|
H2
|
Q2
|
H3
|
Q3
|
S1
|
S2
|
|
14SA-10
|
72
|
0
|
70
|
240
|
65
|
340
|
60
|
380
|
0.0168
|
-0.000117
|
����֪�ĸ�����(bi��o)ֵ����ʽ��12a����������ɵã�
����ʽ��������������ã�S1=0.0168; S2=-0.000117
���Y(ji��)��S1������S2ֵ����ʽ��12b������ԓˮ�õ�Q-H�����������̞�
H=72+0.0168Q-0.000117Q²
����ʽ�cԓˮ���b�õĹܵ�������������ʽ��5��(li��n)������������乤�r�c��Q�����H��ֵ������ |